Другие конечно-разностные методы. Применение конечно-разностных методов

Другие конечно-разностные методы

Существует множество других конечно-разностных схем, сочетающих преимущества явного и неявного подходов. Одной из наиболее известных среди них является схема чередования (hopscotch method), в которой явный и неявный методы применяются поочередно. Этот подход проиллюстрирован на рис. 17.18. В каждый момент времени сначала выполняются все вычисления в "явных узлах". Затем выполняются вычисления по "неявным узлам", причем они не требуют решения системы уравнений, поскольку значения в смежных узлах уже известны.

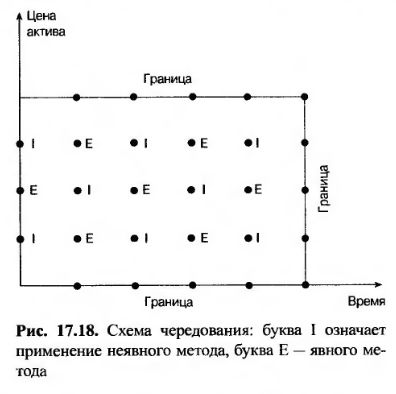
Схема Кранка-Николсона (Crank-Nicolson scheme) является усреднением явного и неявного методов. Для неявного метода уравнения (17.27) приводят к следующим формулам.

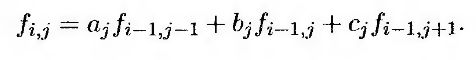
Для явного метода уравнения (17.34) записываются иначе.

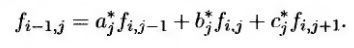
Усредняя эти уравнения, получим схему Кранка-Николсона.

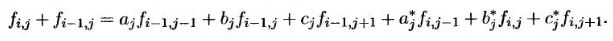
Введем следующее обозначение.

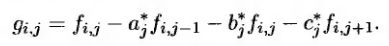
Тогда схему Кранка-Николсона можно записать так.

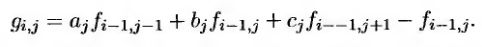
Отсюда следует, что реализация схемы Кранка-Николсона эквивалентна реализации неявного конечно-разностного метода. Преимущество этой схемы заключается в том, что по скорости сходимости она превосходит как явный, так и неявный методы.

Применение конечно-разностных методов

Конечно-разностные методы можно применять для оценки любых деривати-вов, стоимость которых определяется с помощью биномиальных или триномиальных деревьев. Таким образом, конечно-разностные методы позволяют оценить как американские, так и европейские деривативы, но их трудно использовать в ситуациях, когда выигрыш зависит от всей предыстории базовой переменной. Если выигрыш зависит от нескольких базовых переменных, предпочтительнее выглядит явный метод, который выполняется быстрее других. В таком случае сетка, изображенная на рис. 17.15, становится многомерной.

Метод вычисления греческих коэффициентов с помощью конечно-разностных схем практически не отличается от их вычисления с помощью деревьев. Коэффициенты дельта, гамма и тета можно вычислить непосредственно по сеточным значениям f_i,j. Для определения коэффициента вега необходимо немного изменить волатильность и повторно вычислить стоимость дериватива, используя ту же разностную сетку.