|
Казначейские обязательства котируются либо по цене, либо по доходности. Цена представляет собой приведенную стоимость будущих потоков денежных средств от выплаты процентов и номинала. Коэффициент дисконтирования, используемый для вычисления приведенной стоимости, это доходность до погашения облигации. Доходность до погашения (YTM), или валовая доходность до погашения, является наиболее часто используемой мерой доходности. Эта формула учитывает концепцию сложных процентов.


Другими словами, для первого потока денежных средств, представленного ниже, коэффициент дисконтирования вычисляется как величина, обратная 1 + YTM или 1/1,0817 = 0,924471. Второй поток денежных средств составит 1/(1,0817)2 и т.д. Например, 4-летняя казначейская нота с купоном 8,50% и текущей доходностью 8,17%, как показано в табл. 4.1, будет стоить:

Если цена не учитывает накопленного процента по инструменту, то ее называют «чистой ценой». Если облигация куплена в ходе купонного периода с учетом накопленного процента, то цена называется «полной». На большинстве рынков котировка осуществляется в «чистых ценах».
Следует быть очень осторожным в использовании терминологии применительно к различным инструментам сделок. Термины, верные для одного рынка, могут быть неправильными для другого. Примером этого является доходность. Доходность может быть текущей, простой доходностью до погашения или доходностью до погашения (включая изменение рыночной цены бумаги). Для краткосрочных казначейских векселей существует эквивалентная доходность, но здесь мы сосредоточимся только на облигациях.
Текущая доходность может обозначаться рядом терминов (current yield, flat yield, income yield, running yield). Хотя ее вычисление не представляет сложности, она не является такой же точной мерой, как некоторые другие виды доходности, поскольку она не учитывает удорожание или обесценение капитала. Она полезна для оценки доходности при длительных сроках погашения, когда эффекты прироста или потери капитала малы. Текущая доходность соответствует сумме годового дохода от инвестиций, равных номинальной цене облигации: ее можно вычислить с помощью следующего уравнения:
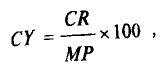
где CY – текущая доходность в %; CR – купонная ставка; MP – рыночная цена. Следовательно, в вышеприведенном примере текущая доходность 4-летней казначейской ноты с купоном 8,50% и равной 101,09 составит:
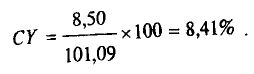
Второй встречающейся мерой доходности является простая доходность до погашения. Она учитывает время до погашения, но не учитывает сложный процент.
Простая доходность до погашения используется на японском фондовом рынке. Она вычисляется по формуле:
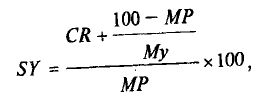
где SY – простая доходность до погашения в %; CR – купонная ставка, My – срок до погашения в годах; MP – рыночная цена. Следовательно, для того же примера простая доходность до погашения 4-летней ноты равна:
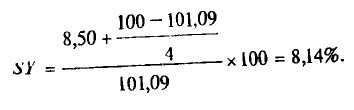
|